El interés es la cantidad que se paga o se cobra, según el caso, por el uso del dinero. Intervienen tres factores importantes en el cálculo del interés, estos son, el capital, la tasa de interés y el tiempo. Verás cada uno de ellos con más detalle durante el artículo.
¿Qué es el interés compuesto?
El interés compuesto consiste en calcular el interés sobre el capital inicial y también el interés de los intereses acumulados de períodos anteriores de un depósito o préstamo. El interés compuesto se puede considerar como » intereses sobre intereses» , y hará que un depósito o préstamo crezca a un ritmo más rápido que el interés simple , que es un interés calculado sólo sobre la cantidad principal.
Por otro lado, el interés compuesto se aplica tanto a los préstamos como a las cuentas de depósito.
La velocidad a la que el interés compuesto se acumula depende de la frecuencia de la capitalización; cuanto mayor es el número de períodos de capitalización, mayor es el interés compuesto. Es decir, el importe de los intereses compuestos que se devengan de 100€ invertido a un 10% anual es menor que si invertimos 100€ al 5% semestral durante el mismo período de tiempo.
Diferencias entre interés simple e interés compuesto
Imagina que inviertes 10.000€ al 8% de interés simple. Esto significa que cuando haya pasado un año se agregan 800€ a la cuenta. En el segundo año se generan otros 800€ en intereses, y lo mismo ocurre con el tercer año, el cuarto año y así sucesivamente.
Si en lugar de interés simple, la inversión es al 8% de interés compuesto, no hay diferencia en los intereses percibidos el primer año, pero diferente para el resto. El primer año se reciben 800€ como lo sucede con el interés simple. Sin embargo, es a partir del segundo año donde comienza a ser diferente. En el segundo año, el interés del 8% se calcula sobre el nuevo saldo 10.800€, no solo sobre los 10.000€ originales. Esto genera unos intereses para el segundo año de 864€, que luego se agrega al principal al calcular los intereses para el tercer año.
¿Cuál es la fórmula del interés compuesto?
La tasa de interés compuesto se expresa normalmente como un porcentaje. Desempeña un papel importante en la determinación de la cantidad de intereses sobre un préstamo o inversión.
La cantidad de interés que se paga o se cobra depende de tres cantidades importantes: El capital, la tasa de interés y el tiempo, que explicaremos a continuación con un ejemplo.
La Fórmula del interés compuesto es:
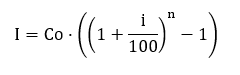
El capital inicial (Co), es la cantidad de dinero que se invierte o que se presta.
La tasa de interés (i), es la cantidad de interés expresado en tanto por ciento por unidad de tiempo.
El tiempo (n), es el tiempo que transcurre entre el momento de la inversión o préstamo y la devolución o pago.
También puedes usar esta otra fórmula, cuando tengas los datos.
I = Capital final – Capital inicial
También te puede interesar conocer la fórmula del interés simple
► Fórmula del interés simple y ejercicios resueltos ◄
¿Cómo se calcula el capital final en interés compuesto?
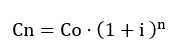
¿Cuál es el capital final de 125.000€ que generan unos intereses de 105.000€ después de 3 años?
Identificamos los datos:
C = 125.000€
i = 10%
t = 3 años
Cn?
Sustituimos los datos en la fórmula para calcular el capital final.
Cn = 125.000 · (1+0,1)^3 = 166.375€
El capital final que se obtiene al invertir 125.000€ durante 3 años con una tasa de interés del 10% es de 166.375€.
¿Cómo se calcula el tiempo en interés compuesto?
Con frecuencia necesitamos calcular el tiempo que tiene que estar una cantidad invertida para que produzca un determinado interés.
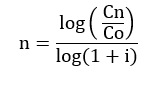
¿Cuánto tiempo tiene que estar un capital de 250.000€ a una tasa de interés del 2,5% anual para que se convierta en 320.000€?
Identificamos los datos:
Co = 250.000€
Cn = 320.000€
i = 2,5%
Sustituimos los datos en la fórmula para calcular el tiempo.
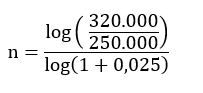
n = 9,99 años.
El tiempo que hay que invertir 250.000€ para que se conviertan en 320.000€ a una tasa de interés anual del 2,5% son 9,99 años.
¿Cómo se calcula la tasa de interés en interés compuesto?
Al igual que ocurre con el tiempo, en ocasiones necesitamos saber la tasa ala que debemos imponer un cierto capital, para que al final de un periodo consigamos un determinado capital final o unos intereses determinados.
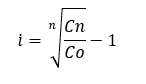
¿Qué tasa de interés ha tenido una inversión de 200.000€ si al final de 5 años ha recibido 350.000€?
Identificamos los datos:
Co = 200.000€
Cn = 350.000€
n = 5 años
Sustituimos los datos en la fórmula para calcular la tasa de interés.
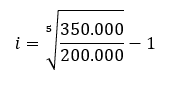
i = 0,1184 · 100 = 11,84% anual
La tasa de interés a la que hay que invertir 200.000€ para que dentro de 5 años nos dé un capital final de 350.000€ es de 11,84%.
¿Cómo se calcula el capital inicial o valor presente en interés compuesto?
Para calcular el capital inicial de una inversión o un préstamo cuando no sabemos su importe, utilizamos la siguiente fórmula.
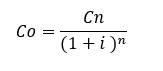
¿Cuál es el capital inicial que al 10,5% anual durante 10 años produce un capital final de 5.000€?
Identificamos los datos:
Cn = 5.000€
n = 10 años
i = 10,5%
Sustituimos los datos en la fórmula para calcular el capital inicial.
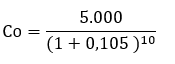
Co = 1.842,24€
El capital inicial que al 10,5% anual durante 10 años produce un capital final de 5.000€ es de 1.842,24€.
Fórmula del interés compuesto en días meses y años. Equivalencias fórmula del interés compuesto
Estas fórmulas están muy bien si la tasa de interés y el tiempo están expresados en la misma unidad, es decir, si el interés es anual y el tiempo está expresado en años. Pero, ¿qué ocurre cuando no coinciden? en ese caso tienes que usar la siguiente fórmula.
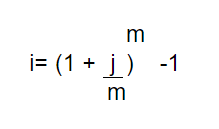
Ejercicio interés compuesto
Supongamos que estas invirtiendo 20.000€ al 1,5% de interés compuesto trimestral, durante 20 años. En este caso lo primero que tenemos hacer es pasar los años a trimestres. N serían 80 trimestres, ya que 1 año tiene 4 trimestres. A partir de esta información, podemos calcular el valor final de la inversión después de 20 años.
Cn = 20.000(1+0,015) ^80 = 65.813,26€
Vamos a invertir 5.000€ en una entidad financiera que nos remunera el capital al 12% nominal y nos da a elegir el intervalo de tiempo en el que queremos que nos liquide los intereses, ¿cuál elegiríamos?
a) Meses
b) Trimestres
c) Semestres
d) Años
Para saber que intervalo de tiempo nos conviene, vamos a aplicar la fórmula de los tantos equivalentes:
Meses -> i = (1+0,12/12) ^12 -1 = 12,68%
Trimestres -> i = (1+0,12/4) ^4 – 1 = 12,55%
Semestres -> i = (1+0,12/2) ^2 -1 = 12,36%
Años -> i = (1+0,12) – 1 = 12%
Si observamos los resultados obtenidos comprobamos, que partiendo de un mismo tanto nominal, obtenemos un tanto anual equivalente distinto en cada caso. De forma que, cuanto más corto sea el periodo de liquidación mayor TAE conseguimos.
Por tanto, la pregunta que nos hacíamos en el enunciado de este ejemplo es fácilmente contestable: a igualdad de tanto nominal, siempre preferimos invertir en aquellos que liquiden intereses con mayor frecuencia, es decir elegimos por meses.
Ejercicios del cálculo de interés en capitalización compuesta (o interés compuesto)
La mejor manera de comprobar si te ha quedado claro es hacer estos ejercicios por tu cuenta antes de mirar las respuestas.
1.Invertimos 3.000€ durante 5 años al 0,35% de interés compuesto. mensual.
- ¿Cuánto habrá en la cuenta al final de los 5 años?
- ¿Cuánto interés se ha ganado?
2. Invertimos 5.000€ en un depósito durante 18 meses pagando el 1,3% compuesto trimestral.
- ¿Cuál es el valor final?
- ¿Cuál es el importe del interés generado?
3.Calcula el montante compuesto y el interés compuesto sobre el capital prestado 20.000€ al 6 % compuesto anual durante 3 años.
4.Encuentra el capital final, que se obtiene a partir de un capital inicial de 2000€ a un interés compuesto trimestralmente del 6% durante 5 años.
Soluciones:
Respuesta ejercicio 1
Co = 3.000€, n = 5 años i =0,35% mensual
Cn = 3.000(1+0,0035) ^60 = 3.699,68€
Pasados 5 años los 3.000€ invertidos se convierten en 3.699,68€
I = 3.699,68€ – 3.000€ = 699,68€
Respuesta ejercicio 2
C0 = 5.000€, n= 18 meses, i = 1,3% trimestral
Cn = 5.000(1+0,013) ^6 = 5.402,90€
I = 5.402,90€ – 5.000€ = 402,90€
Respuesta ejercicio 3
Co= 20000€, i = 6 %, n = 3
Utilizando la fórmula
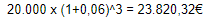
El interés compuesto = 23820,32€ -20000€ = 3.820,32€
Respuesta ejercicio 4
Capital inicial = 2.000, i = 6 %; n = 5 x 4 = 20 trimestres
2.000 · (1 + 0,06) ^20 = 6414,27€
El interés compuesto =6414,27€ – 2000€ = 4414,27€



Yo estoy haciendo los ejercicios y los resultados que me dan no coinciden con esos. Por ejemplo, el ejercicio 2 me da 5100 euros, lo cual me parece coherente porque es muy poca la tasa de interés.
Le agradecería si pudiera revisarlos nuevamente a ver si coincide con mi resultado.
Gracias.
Buenos días Andrea,
Hemos revisado los ejercicios y los resultados son los correctos. Dinos como has realizado las operaciones para poder ayudarte.
Saludos
Esta claro los pasos que hay que hacer felicitaciones por brindar ayuda al que lo nesecitamos gracias
Hola quisiera saber si se puede calcular la tasa de interes anual compuesto, apartir del valor inicial, el valor final y el periodo.
Es decir si me prestan 12500 euros a 7 años y al final pago 23440 euros.
el interes compuesto anual seria ??
Buenos días Humberto,
Sí se puede calcular la tasa de interés anual compuesto con los datos que me has indicado, para ello solo tienes que utilizar la fórmula del cálculo del tanto de interés
i =(cn/c0)1/n – 1
Vamos a resolver tu ejemplo para que lo veas más claro.
El capital inicial C0= 12500
El tiempo n = 7 años
El capital final Cn = 23440
i = ((23440/12500)^(1/7)) -1
Siendo la tasa de interés de 0,093973493, es decir 9,40%.
Saludos
Muchas gracias por la explicación. Me resultó de mucha utilidad.
Muchas gracias por publicar información, me ha ayudado mucho.
Muchas gracias por tu comentario Violeta
Una persona deposita 200 um (unidades monetarias) en un banco que garantiza un tipo de interés compuesto anual del 6% ¿Qué interés recibe al cabo de 21 meses?
Me pueden ayudar con esto por favor
Hola Andy,
Lo primero que tienes que hacer es tener todos tus datos expresados a la misma unidad de tiempo. 21 meses son 1,75 años.
Ahora utilizando la fórmula del interés compuesto Cn = Co x (1 + i )^ n sustituimos los datos.
Cn = 200 x (1+0,06)^1,75 -> Cn = 221,47 u.m.
La diferencia entre el capital invertido y el capital final es el interés. Cn – Co = I
221,47 – 200 = 21,47.
Por lo que el interés que recibe al cabo de 21 meses son 21,47 u.m.
Saludos
A mi si me salieron todas😁😁!!! Gracias !! Solo quisiera saber las fórmulas ..
Muy bien Jose. ¿A qué formulas te refieres?
Todo me ha cuadrado a la perfección, obviando el redondeo por centavos que han hecho verdad?
De ahí todo calza y encaja, gracias. y no no soy un bot xdd en verdad está muy weno.
genial me has ayudado bastante es que tengo que presentar ejercicios faciles de interes compesto y resueltos a ver si me podías colaborar
Lo primero que tienes que hacer es tener todos tus datos expresados a la misma unidad de tiempo. 21 meses son 1,75 años. ¿como es la operación para convertir los 21 meses a1,75 años?
gracias!
Haces una simple regla de 3, si en un año hay 12 meses, cuantos años (X) habrán en 21 meses
1 año—–> 12 meses
X———-> 21 meses
Haces el cruzamiento y te queda= 12meses.X=1año.21 meses; puedes si o no considerar el 1 año, es irrelevante
X=21 meses / 12 meses; X=1.75 años
Y eso es todo
gracias, estaba considerando 365 días (año), considerando 360 días, ya me quedo claro.
saludos!
Hola muchas gracias a mí salieron todas y la verdad he entendido mucho mejor con tigo, que con mi profesor. Bendiciones
Muchas gracias…me ayudo bastante
Por favor ayúdame con esto, por ejemplo:
calcule el capital final que obtendremos transcurridos tres años por el depósito de $ 2.500 al 6,25% de interés compuesto anual, según la liquidación de intereses sea semestral, trimestral o mensual
Realizas la fórmula: 2500(1+0.0625)^3=2.998,65
Buenas, cómo saco el 10% de los intereses?
¿Cuál es el capital final de 125.000€ que generan unos intereses de 105.000€ después de 3 años?
Identificamos los datos:
C = 125.000€
i = 10%
t = 3 años
Cn?
Sustituimos los datos en la fórmula para calcular el capital final.
Cn = 125.000 · ( 1+0,1)^3 = 166.375€
si me puede ayudar a responder este ejercicio por favor es que me cuesta trabajo entenderlo.
francisco adquiere un crédito por la siguiente por la siguiente manera
1. un pago de 35,000 dentro de 3 meses.
2. y otro pago de 25,000 al 25% capitalizable bimestral al 7 mes.
3. un ultima pago por 30,000 al año.
francisco decide liquidar en 2 pagos, uno dentro de 4 meses y otro en el mes 11 de 48,000 la nueva transacción se realiza con una tasa del 25% capitalizable trimestralmente.
Hola!! Alguno podría explicarme por favor como se deduce que el interes anual es del 10% en este ejemplo?
¿Cuál es el capital final de 125.000€ que generan unos intereses de 105.000€ después de 3 años?
Identificamos los datos:
C = 125.000€
i = 10%
t = 3 años
Cn?
hola buenas noches me podrian ayudar con este ejercicio
Cuanto deberia pagar una persona dentro de 3 años por una deuda que adquirio de $15.600.000, si la tasa que le cobra la entidad es del 3,2% capitalizable bimestralmente ?
Usas la fórmula: Cn(1+i)^t
Reemplazas por los datos.
156000(1+0.032)^18
Respuesta:27501.67
Si invertimos un capital de 10.000,00€ y, transcurridos 32 trimestres, retiramos en concepto de capital e intereses 21.435,89€.Cual sería el tipo de interés compuesto semestral al cual estría invertido el capital?
(21.435,89/10.000)^(1/16)-1= 0.488 x 100 = 4.88% semestral
16 semestres / 2 pagos al año = 8 años
32 trimestres / 2 = 16 semestres
4.88% semestral
Hoygan me podrían alludar con ésto
Panchita invirtió cierta cantidad de dinero durante ocho años y medio a 23 % convertible trimes-
tralmente; determinar:
a. La frecuencia de conversión
b. La tasa de interés por periodo
c. El número de periodos de conversión
d. Fc = 12 (meses del año)/3(porque es trimestralmente) = 12/3 = 4
e. i = ta
fc
= 0.23
4 =0.06
f. n = (# de años)(fc) = (8.5 años)(4) = 34 trimestres
Ya que 6 equivale a “medio año”/3 “trimestralmente” = 6/3 = 2, entonces es 8 años × 4 trimes-
tres +2 trimestres = 34.
¿Cuál es el monto compuesto que resulta de invertir $ 420 000.00 por seis años ocho meses a
55 % convertible bimestralmente?
fc = 12 = 2 = 6
i = .55/6 = .09
n = 6(6) = 36 + 4 = 40
S = C(1 + i)
40
S = $ 420 00.00(1 + .09)
40
S = $ 420 000.00(31.41)
S = $ 131 922.00.
buenos días espero que me puedan ayudar a saber saber como se calcula: Se prestan $45000 al 5% de interés compuesto durante 8 años. ¿En cuanto se convertirá la cantidad prestada y cuál es el interés compuesto?
AYUDA PLEASE ,
Para construir un departamento con un presupuesto de 525 mil pesos, al arquitecto Castillo se lo distribuyen de la forma siguiente: $ 150 000 un mes antes de comenzar las obras, $ 200 000, 15 días después de iniciarlas y $ 175 000, 28 días después del anterior.
Se depositan en una institución que bonifica intereses del 8.4% anual capitalizable por meses y las disposiciones se realizan de la forma siguiente: la primera por $ 130 000, 15 días antes del inicio y $ 200 000, $ 90 000 y $ 85 000, al final de cada uno de los siguientes tres meses, respectivamente, entonces la terminación, luego de 4 meses de haber comenzado dispondrá de $ _________
Un gusto poder comunicarme con ustedes, muy buen articulo. ¿Sabrán porque la constante es Uno?
Vanessa, muchas gracias por este aporte. Todo muy claro y bien explicado. Como sugerencia deberías pensar en adjuntar un enlace para descargar la información que vemos en este tema en formato pdf. Para así poderlo tener a la mano libremente. Saludos desde Venezuela.
¿cual seria el interés compuesto de un préstamo de $1.500.000 a una tasa de interés mensual de 3% con un plazo de 8 meses ?
Alguien podría ayudarme a resolver este ejercicio
Cierta cantidad se invierte con una tasa de interés del 10.03% compuesta bimestral. El tiempo en que se duplicará dicha cantidad está:
a) entre 83.63 y 83.63 años
b) entre 41.81 y 41.82 años
c) entre 6.96 y 6.97 años
d) entre 83.10 y 83.11 meses
Hola me pueden ayudar con esta pregunta estoy en un examen, porfavor en el interés compuesto para dinero destinado al ahorro si es rentable ya que el interés compuesto se capitaliza el monto inicial según la cantidad de tiempo por ejemplo si ponemos 1000 soles a un interés de…
Porfavor ayúdenme
buenas noches cómo puedo calcular Se deposita la cantidad de $ 5’352,500.50 en dos instituciones bancarias bajo la siguiente prerrogativa se deben de depositar $ 6.00 de cada $10.00 en la primera el resto en la segunda . La primera paga 3% de interés compuesto capitalizable bimestralmente; la segunda 3.5% de interés trimestralmente. A un periodo de 7 semestres.
(1/2 punto) A cuánto asciende el monto final obtenido en la primera institución bancaria.
Me gustaría que me diera la formula para calcular lo que debo pagar mensualmente en una amortización- En algunos textos lo definen como r
He adquirido una propiedad con valor inicial de 15000000 de pesos con un interés compuesto de 1% mensual que se debe cancelar en 15 años. el pago se debe hacer con cuotas mensuales iguales. deseo saber cual es el valor de la cuota mensual
Que bien, todo claro y sencillo, Vanessa. Si me podrías ayudar con este problema.
Si ahorro mensual, 200 soles por 15 años, al termino recibo 45,000 soles.
A que tasa de interés compuesto estuvo?
Me ayudas con las fórmulas y resolución.
Muchas Gracias.
Hola fernando. Creo que al ahorrar 200 mensuales por 15 años tendrias un capital inicial de 36,000 soles (200x12x15). Entonces, aplicando la formula, para así despejar el interes compuesto en porcentaje es: 45,000=36,000(1+i%)^15. Despejando eso, te sale que el interes compuesto en porcentajes es de 1.4987%. Esto lo puedes comprobar reemplazando este interes hallado en la formula y veras que te sale los 45,000 soles
hola alguien me puede ayudar con esto porfavor.
Invertimos $ 5.000 durante 7 años al 0,35% de interés compuesto. mensual.
¿Cuánto habrá en la cuenta al final de los 5 años?
¿Cuánto interés se ha ganado?
Según tengo entendido, habrá C-final = $5010.21 y habrá generado $10.21. La formula que utilicé fue I = 5000(1+0.35%/12)^5
hola chicos y chicas, saludos para todos. Quiero felicitar a la persona que escribio este articulo, esta muy interesante…
Me podían ayudar con este ejercicio
Ramon deposito $72000 con una taza de interés anual del 7% durante 5 años .¿si habría sido a un 14% anual ¿ su ganancia habría sido el doble ? Argumenta la respuesta
No exactamente aunque el resultado se aproxima.
72000 x (1+0.07)^5 = $ 100938 I= $ 28.938 el doble de esta cantidad es $ 57.876
72000 x (1+0.14)^5 = $ 138629 I= $ 66.629
Si aplicamos el 14% anual, el resultado es más del doble por el interés compuesto.
excelente podria apoyarme a desarrollar ejercicios gracias
Por favor, necesito de vuestra ayuda para solucionar el siguiente problema:
La empresa «XY» hoy ha recibido $ 13.425.000, fruto de una inversión realizada hace 3 años, que pagó una tasa de interés del 15 % anual, con capitalizaciones de intereses trimestrales. ¿ Cuanto fué el valor de la inversión inicial?
Agradecido
me podrian ayudar con este ejercicio por favor
4. Si Ud. invierte el día de hoy $ 50000 dentro de 1 años le pagarán $25000, al 2do año 10000 y durante 3 años adicionales $15000. Calcule la tasa de interés compuesto anual que rigió la operación
Se depositan 1000 al 5% anual de interés compuesto ¿cual es el capital final al cabo de 2 años?
Me ayuda
Hola, necesito si me pueden ayudar con unos ejercicios por favor:
1. ¿Cuánto dinero tendré en 3 meses, si deposito en un banco, la cantidad de 60000 soles a un 13% efectiva anual?
2. Una persona desea obtener 30000 soles dentro de 2 años. ¿Cuánto debe de invertir hoy para obtener dicho monto, si la tasa de interés que le da la entidad bancaria es de 18% anual con capitalización mensual?
Si me podrían ayudar por favor gracias.
Me parece muy util, la información que brindan,quisiera saber cómo, se obtiene el capital inicial en interés compuesto, cuando me dan el capital final
Digamos que usted quiere invertir 6000 dólares con un 4% de interés compuesto anual al cabo de 8 años ¿Cuánto tendría de saldo si sus intereses se capitalizan anualmente y mensualmente?
Disculpe como puedo saber el importe de un prestamo si mi capital final es de 418,000 y los intereses ingresados son de 116,000?
• ¿A qué tasa de interés anual se deberá invertir US$4.500 para
que al cabo de tres años se logre acumular US$8.000,
sabiendo que durante los 17 meses anteriores a la fecha del
saldo la tasa de interés fue del 9,5% anual?
Pueden ayudarme: en cuanto tiempo producen igual monto dos capitales de $us. 10000 y $us. 25000 colocados a la tasa de interes del 5% y 3% de interés anual.
me podrían ayudar a resolverlo: Un inversionista desea saber ¿Cuál es el monto de una inversión de $10,000 al cabo de 3 años? Si se deposita en una cuenta bancaria que paga el 30% de interés anual convertible trimestralmente, hacer la comprobación
Hola Vannesa se que ya es mucho tiempo después pero porfavor espero que mires esto necesito que me ayudes a saber estos ejercicios en interés compuesto son algunos que están en interés simple pero esto es un tema muy complicado y no lo entiendo porfa ayudame:
1- Calcula el interés simple de un capital de 24.000€ invertido durante 3 años al 5% anual.
2- Calcula el interés simple de un capital de 29.000€ invertido durante 89 días al 4% anual.
3- Al cabo de un año, el banco nos ha ingresado en nuestra cuenta de ahorro la cantidad de 870€ en concepto de
intereses. Siendo la tasa de interés del 2% anual, ¿cuál es el capital de dicha cuenta?
4- Por un préstamo de 19.000€ hemos tenido que pagar 21.200€ al cabo de un año. ¿Cuál es la tasa de interés que nos
han cobrado?
5- Invertimos un capital de 250.000€ a una tasa de interés anual del 6% durante un cierto tiempo, ha generado unos
intereses de 10.000€ ¿cuánto tiempo ha estado invertido?
6- Hemos invertido durante cierto tiempo un capital de 24.000€ a una tasa de interés simple anual del 5%. Al final
hemos obtenido un capital de 29.000€. ¿Durante cuánto tiempo ha estado invertido?
7- ¿Cuál será el tanto por ciento de interés simple al que debemos prestar un capital para que pasado 30 años, los
intereses generados sean equivalentes al capital prestado?
8- ¿Cuánto tiempo a de pasar para que un capital se triplique al 4% de interés simple?
Hola quisiera saber ¿como se calcula parte de interés y parte de capital en una cuota mensual hipotecaria dependiendo del interes?
La cuota misma esta calculada por la formula francés. Por ejemplo 10000 $ y interés 2% ¿como sera la diferencia si sube inters a 3%?
Gracias
Muchas gracias, soy un profano en materia económica / matemática, sin embargo su explicación ha sido tan clara que me ha sido muy fácil entender todas sus indicaciones para conocer las incógnitas que rodean al interés compuesto.
Un saludo y gracias
me ayudan a resolver este:
¿ Cuanto tiempo se debe esperar para que una inversion al 1.89% mensual incremente en un 40%?
Gracias me ayudaron a comprender muchas cosas… lo visitaré siempre que tenga una duda
Holaaa!! Podrían explicarme por favor como se deduce que el interes anual es del 10% en este ejemplo?
¿Cuál es el capital final de 125.000€ que generan unos intereses de 105.000€ después de 3 años?
Identificamos los datos:
C = 125.000€
i = 10%
t = 3 años
Cn?
un capital de 30000 se coloca al 24% nominal anual con capitalización trimestral durante 5 años. al finalizar al segundo año la tasa de interés se aumenta a 30% nominal anual con capitalizacion mensual. calcular el monto al final de los 5 años
Tengo una consulta con respecto a la formula, ya que en muchos casos veo que no se concidera el (-1) que se encuentra en la formula, pero aqui en los datos brindado si se le considera, quisiera saber porquè.
Mi opinion es sobre dos problemas en que la respuestas una de Vanessa y otra de Isaac por ej. Vanessa eleva el tiempo a 1/7 e Isaac a /16 porque y cuando ocurre esta fracción del tiempo. lo que extraño es que ningun profe dá una explicacion sobre esto pues tambien algunos lo elevan a 1/12 incluso los alumnos se atienden a las formulas y no lo preguntan . Yo ahora pido una respuesta y creo será util a muchos alumnos como yo con mis 90 años quiero ser amigo de las matematicas que nunca entendi mucho. ahora en cambio tengo claro pero me falta lo comentado para resolver problemas de inters compuesto . Atte Lauta.de chile.
Buenas Lauta,
Esta fracción del tiempo se utiliza para que toda la fórmula esté expresada en el mismo tiempo, si quieres saber el interés anual todo tiene que estar en años, si lo quieres saber en meses, lo mismo, todo expresado en meses. Por eso a veces se eleva el tiempo a 1/7 o 1/16, etc. Cuando quieres que esté en meses se divide 1/12 porque un año tiene doce meses, si son trimestres 1/4, porque un año tiene 4 trimestres, si son semestres 1/2, porque un año tiene dos semestres y así con todos los tiempos.
Saludos
Mil gracias Vanessa una rica explicación Atte Lauta Chile
Hallar el monto compuesto de $3000 en 8 años el cual está colocado a una tasa de interés 5%anual
buenas tarde me ayudarías con este problema
La empresa Los Lirios, C.A, dispone de una letra de cambio de valor
nominal 3.000.000 de bolívares con un vencimiento dentro de tres
años. Calcula el efectivo que recibirá por dicha letra en el caso que
quiera descontarla en una entidad bancaria que paga un 6% de
interés racional compuesto.
se debe saber que capital debe colocarse durante 3 años en una financiera que paga el 12 % capitalizable trimestralmente, si se desea cobrar un monto de 124 000
En la Fórmula del interés compuesto en días meses y años. Equivalencias fórmula del interés compuesto, las variable sj y m que representa?
de antemano gracias y saludos.
Alguien puede ayudarme en este problema:
un capital de 54.875 eur ha estado invertido en régimen de capitalización compuesta generando un capital final de 164.625 eur.
un segundo capital invertido con el mismo tipos de interés compuesto, ha generado el mismo capital final, pero en la mitad de tiempo.
¿Calcular el importe de este segundo capital.?
Me he bloqueado y no me sale nada…. gracias
Muchísimas gracias, muy útil y fácil de entender
buenas tardes me podrian ayudar con una tarea .existe una capital de $4500 que estuvo invertiendo ,durante el semestre si la tasa de interes del 2% efectivo anual¿cual fue su monto o valor a futuro?
Buenos días,
Si tienes un capital inicial (valor presente, Co) de $4500 y estás invirtiendo durante un semestre a una tasa de interés efectivo anual del 2%, puedes calcular el valor futuro (Cn)utilizando la fórmula del interés compuesto:
Cn = Co * (1+i)^n
Donde:
Cn es el valor futuro.
Co es el valor presente o capital inicial ($4500 en este caso).
i es la tasa de interés por período (tasa efectiva anual dividida por el número de períodos por año).
n es el número total de períodos.
Dado que la tasa de interés es del 2% efectivo anual y estás invirtiendo durante un semestre, la tasa de interés por período (i) sería 0.02/2= 0.01 y el número total de períodos (n) sería 1 (un semestre).
Sustituyendo los valores en la fórmula:
Cn=4500×(1+0.01)^1
Cn=4500×1.01
Cn=4545
Por lo tanto, el valor futuro de la inversión después de un semestre sería aproximadamente $4545. Esto significa que tu capital de $4500 habría crecido a $4545 al final del semestre con una tasa de interés del 2% efectivo anual.
Saludos